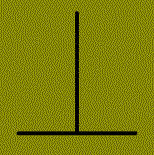| Retour | Les illusions d'optique | Retour |
L'image "physique" formée au fond de l'œil, analysée point par
point, puis transmise au cerveau sous forme de messages codés est en principe
la même pour tous.
Ce sont les zones visuelles du cerveau qui analysent ces signaux et nous
donnent une représentation de l'objet perçu.
L'interprétation qu'en fait le cerveau peut parfois être ambiguë. Ces "erreurs"
d'interprétation sont des illusions d'optique, qui ne sont pas perçues de
la même façon par chacun d'entre nous (nous n'avons pas tous le même "vécu",
ni les mêmes images en mémoire)...
Les
illusions sont les témoins des mécanismes de la vision. Elles confirment
que notre perception du monde est assez éloignée de la photographie. Elle
est le résultat :
-
d'une stimulation des photorécepteurs rétiniens, qui peuvent subir des phénomènes
de fatigue,
- et surtout d'une construction mentale, à partir des messages nerveux reçus, parfois erronés. Le cerveau cherche à mettre du sens partout, même quand il n'y en a pas. Alors, il en fait trop, amplifiant les contrastes, créant contours, couleurs, perspectives, reliefs, mouvements, en fonction de ce qu'il connaît. En effet, malgré une organisation générale commune du cortex visuel, les apprentissages et les expériences acquises diffèrent d'une personne à l'autre, d'où une sensibilité variable à certaines illusions.
-
Explications des illusions optico-géométriques :
Ce sont des illusions formées par des figures géométriques
qui donnent lieu à des erreurs d'estimation, de dimension, d'interprétations,
de courbure, de direction...
Au cours de la seconde moitié du XIXe siècle, des pionniers de la psychologie
expérimentale, comme Delboeuf, Hering, Müller-Lyer et plusieurs autres ont
découvert une grande variété d’illusions dites optico-géométriques auxquelles
ils ont laissé leur nom. Au total plus de 200 illusions géométriques ont
été répertoriées.
|
|
On
considère généralement qu’une illusion géométrique comporte deux éléments
: - un élément "inducteur"qui provoque la déformation |
|
Depuis plus d'un siècle nous avons proposé plusieurs
explications pour les illusions géométriques mais les plus convaincantes
s’accordent sur trois points importants. Tout d'abord, les illusions sont
du domaine perceptif et n’ont rien à voir avec la pensée ou le raisonnement.
En effet, nous savons que la plupart de ces illustrations sont des illusions
géométriques, mais cela ne nous empêche pas de percevoir des déformations.
Ensuite, les illusions ne naissent pas dans la rétine ; elles apparaissent
presque aussi nettement lorsque l'élément inducteur est placé devant un
oeil et l'élément test devant l’autre oeil. Elles prennent donc naissance
dans le système visuel, là où convergent pour la première fois les informations
en provenance de chaque oeil. Enfin, les illusions ne résultent pas du mouvement
oculaire. En effet, elles apparaissent très nettement quand la durée d’exposition
est trop brève pour que l’oeil ait le temps de balayer la figure.
A) CLASSIFICATION DES ILLUSIONS OPTICO-GÉOMÉTRIQUES :
1) La mise en relation de grandeur :
|
De nombreuses illusions produisent une mise en relation
de grandeur des éléments de la figure. Il en résulte généralement
un effet de contraste : la grandeur apparente des éléments les plus
grands est surestimée par comparaison au plus petit et inversement.
Le cas le plus évident est sans doute l’illusion de Titchener (à droite).
On a cependant invoqué à certains moments le principe d’assimilation
suivant lequel, lorsque les différences sont minimes entre les plus
grands et les plus petits éléments, on a tendance à minimiser ces
différences. Il s’ensuit une assimilation d’un élément test à un élément
inducteur plus grand (donc un surestimation de l’élément test) ou
plus petit ( donc une sous-estimation de l’élément test), alors que
le contraste apparaît lorsque la différence entre l’élément inducteur
et l’élément test est plus importante. |
Illusion
de Titchener |
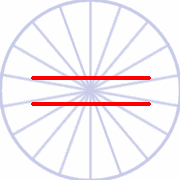
2) La courbure des arcs de cercle:
|
|
La courbure des arcs de cercle varie en fonction de leur longueur. Les arcs court sont vus plus plats que les arcs longs. |
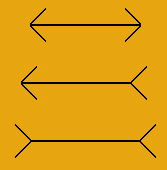
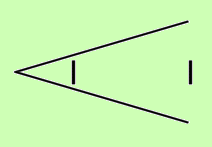
3) Les effets d'angles :
|
|
Les illusions dues à des effets d’angles sont très
nombreuses et elles sont sans doute parmi les plus spectaculaires.
Les scientifiques se sont appuyés sur deux principes pour les expliquer.
Tout d'abord, nous avons tendance à sur-estimer les angles aigus et
a sous-estimer les angles obtus. Nous avons qualifié ceci de principe
d’orthogonalité, étant donné qu’il s’agit dans chaque cas d’une tendance
à ramener l’angle vers un angle droit. Ce principe permet d’expliquer
facilement les illusions de Zöllner (à droite) et de Hering (à gauche),
mais il peut aussi s’appliquer à l’illusion de Poggendorff et à celle
de Müller-Lyer (voir plus haut). Le second principe concerne la tendance
que l’on a à sur-estimer les côtés d’un angle obtus et à sous-estimer
ceux d’un angle aigu. Dans ce cas, l’illusion de Müller-Lyer pourrait
encore servir d’exemple. |
|
4)
La verticalité :
|
Une ligne verticale paraît plus longue qu’une horizontale
de même longueur car le mouvement des yeux qui est lié aux lignes
horizontales est plus facile à exécuter qu’un mouvement vertical.
L’exemple le plus fréquemment cité est le T inversé (à droite), mais
il faut noter que cette forme donne lieu à des effets d’illusion compétitfs
parce que, en plus de la surestimation liée à la verticalité, il y
a un effet de contraste de grandeur produit par la mise en relation
entre la verticale et chaque segment de l’horizontale. On obtient
un pur effet de la verticalité en utilisant plûtot la figure en forme
de L. |
|
5)
La perspective :
|
|
La présence de traits suggérant la perspective entraîne
des illusions de grandeur. À même grandeur physique, une forme paraissant
plus éloignée qu’une autre sera vue plus grande et inversement. On
a tenté de généraliser ce principe à plusieurs illusions. Ainsi, l’illusion
de Ponzo (à gauche), qui pourrait être également considérée comme
une illusion de mise en relation de grandeur, est fréquemment expliquée
par un effet de perspective. |
6) La division de l'espace :
|
|
Un espace qui est divisé ou occupé par de nombreux
éléments apparaît généralement plus grand qu’un espace qui ne l’est
pas. L’exemple typique est celui de l’illusion d’Oppel-Kundt. |
7) Les
illusions de couleurs :
|
|
Les
illusions de couleurs sont nombreuses. L'illusion de couleur de gauche
montre bien ce phénomène. Ce sont les couleurs d'arrière plan qui
vont influer sur l'illusion, en effet à gauche le blanc semble accentuer
la nuance du carré de gauche et le rouge foncé semble diminuer la
nuance du carré de droite. |
|
B) LA PERCEPTION DES ILLUSIONS SELON LES CULTURES :
Les illusions
dépendent non seulement de notre système visuel mais aussi de notre culture
en général. Ainsi, les européens paraissent avoir une illusion de Müller-Lyer
plus forte et une illusion du T renversé moins forte que d’autres groupes
ethniques, en particulier africains.
Nous qui vivons en Occident dans un monde oû les formes
géométriques avec des angles droits prédominent (immeubles aux lignes perpendiculaires,
murs verticaux, plafonds horizontaux ...) avons une très forte tendance
à sur-estimer les angles aigus et à sous-estimer les angles obtus, de manière
à les ramener à des angles droits. C’est pourquoi nous sommes plus sensibles
à l’illusion de Müller-Lyer.
Pour ce qui est de l’illusion du T renversé, une autre
explication s’applique. Comme les peuples africains vivent dans la savane,
qui a un relief très plat, et que leur environnement est pratiquement dépourvu
d’arbres, de maisons ou de poteaux, ils sont donc moins habiletés que nous
à juger les lignes verticales ; c’est pourquoi ils sont plus facilement
bernés par l’illusion du T renversé.
-
Explications des illusions artistiques :
Ces illusions ne sont pas des manifestations d'erreurs
d’interprétations du système visuel humain mais plutôt la conception de
l’oeuvre qui induit notre oeil en erreur.
Il y a plusieurs
groupes :
- Un groupe
qui illustre l’illusion, les dessins font naître des interprétations visuelles
qui sont très différentes des propriétés des éléments représentés.
- Des groupes portant sur l’ambiguïté, chaque dessin
peut donner lieu à au moins deux interprétations visuelles qui s’excluent
mutuellement.
- Des groupes sur l’impossibilité, des parties différentes
de chacun des dessins suscitent des interprétations incompatibles entres
elles. Tous les objets de cette catégorie ne pourraient pas exister ou il
serait fortement improbable qu’ils existent dans la réalité.
-
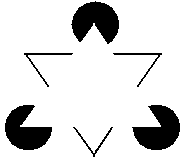
Les contours subjectifs :
|
|
Ce phénomène consiste à percevoir des figures qui se
détachent de leur fond bien qu'aucun trait ne soit tracé pour délimiter
celles-ci. Ces figures nous paraissent aussi plus claires ou plus
sombres que leur fond. |
|